We have theoretically designed a new class separation measurement.
The class separation is a distance. It evaluates the separation of K classes in a D dimensional space. It returns a separation value ranging in the [0,1] interval. A value of 1 indicates that the classes are fully separated (i.e. the K classes do not overlap at all). A value close to 0 indicates low separation of classes (i.e. high overlap).
Some of the typical machine learning applications are classification or cluster validation. In those cases, a maximum separation is preferred as it will lead respectively to higher classification accuracies and better cluster definition. Figure 1 shows the Class Separation Metric (CSM) concept in 1D. Three probability distribution functions (PDFs) have a partial overlap. The portions of the PDFs that do not overlap define the CSM value.

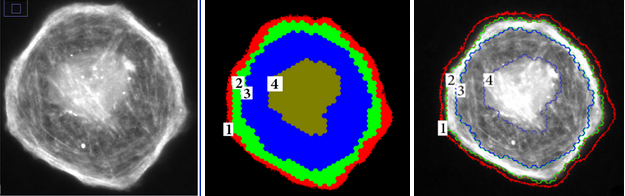
We used the class separation metric to automate the feature selection process by searching for a subset of features that maximizes class separation. It was used to segment epifluorescence microscopy images of cells at a sub-cellular level, into 4 meaningful regions (see Figure 2). Out of the initial 15 features, 2 features were identified as the best subset of features, visualized in Figure 3 after normalization. Each color correspond to one of the 4 classes (cell regions).

In the more general case with multiple classes and multiple dimensions, here is our definition of the CSM:
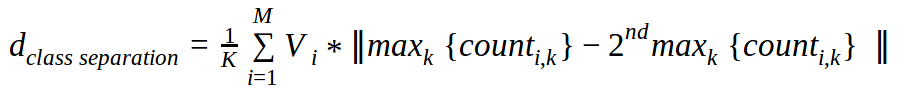
where
Julien Amelot, Peter Bajcsy and Mary Brady, “Class Separation Measurements For Multi-dimensional Points from Highly Overlapping Classes”, Journal of Machine Learning Research, Under review, March 2014
Peter Bajcsy
[email protected]
Phone: 301.975.2958